Il est établi par le calcul et par des mesures expérimentales que l’effet Coanda: déviation d’un jet qui suit une paroi courbe, s’explique par une cause purement inertielle: le gradient de pression qui l’attire vers la paroi: il n’est pas produit par la viscosité mais au contraire limité par elle, par la remontée de pression longitudinale le long de la paroi dans la couche limite qui finit par décrocher le jet de la paroi.
J’ai pu évaluer ce détachement de la couche limite par le calcul grossier que j’ai présenté dans l’article: “Calcul de la déviation d’un jet par une paroi courbe”, situé dans le thème: Science, Fluidique, présenté à la Société Hydrotechnique de France en 1966.
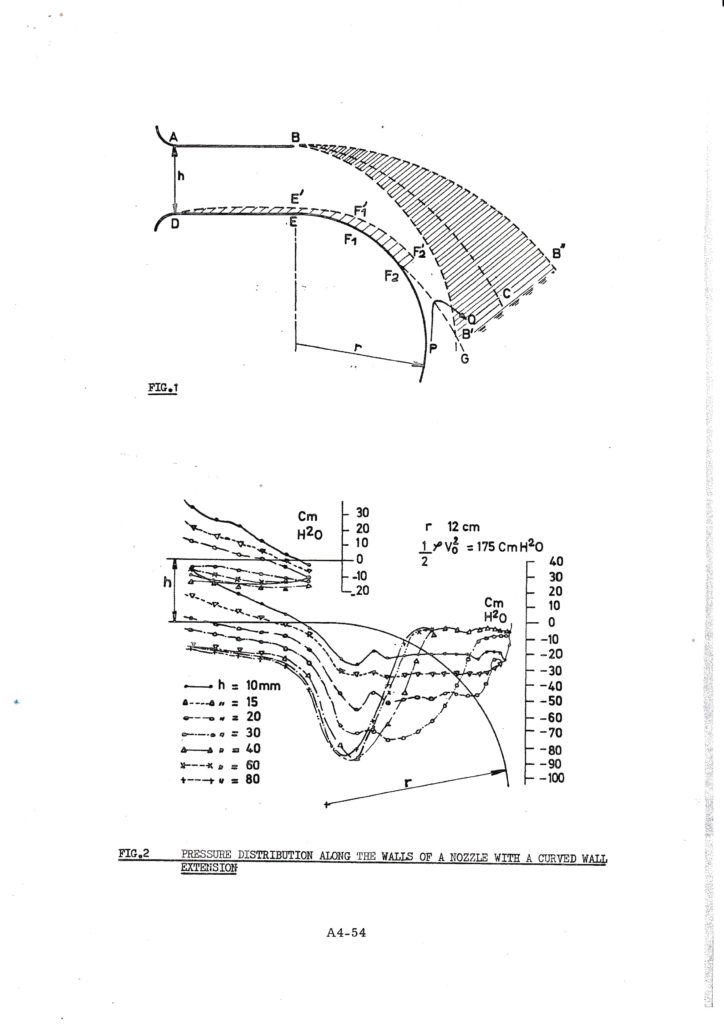
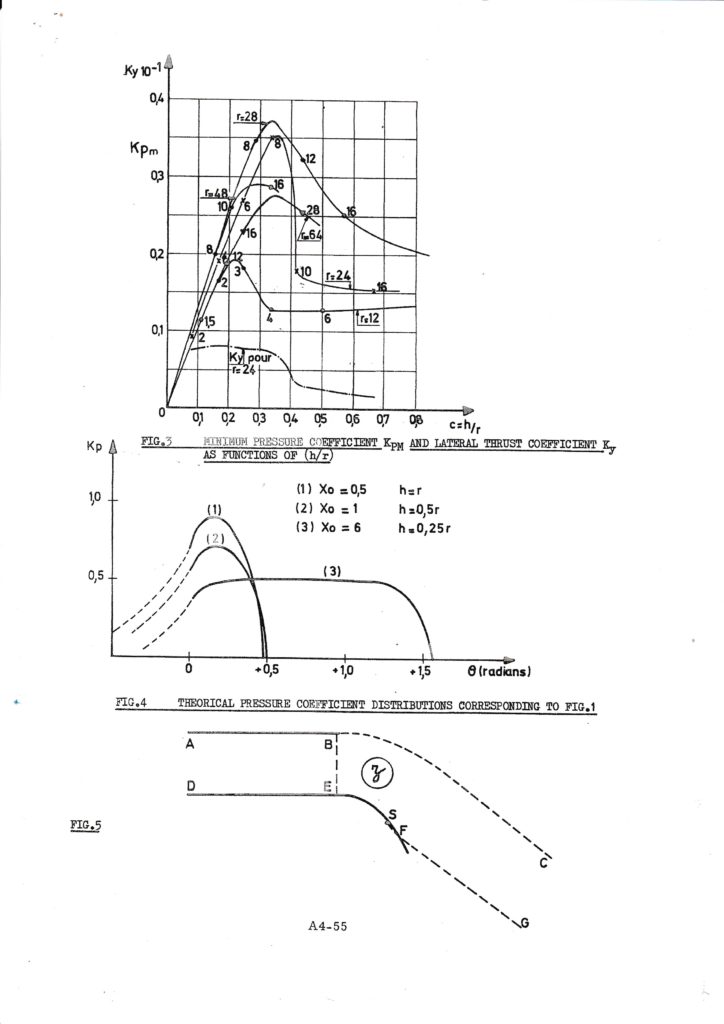
Le jet de largeur h, nombre de Reynolds Re, attaché à une paroi convexe de rayon de courbure r, le long d’un arc rγ, est décollé par l’effet du gradient de pression sur la couche limite.
Les formules obtenues montrent que l’angle d’attachement γ est pratiquement constant si Re r/h est inférieur à une valeur critique, et augmente au delà comme:(r²h²Re) exp1/6. Elles confirment les résultats expérimentaux obtenus par l’auteur avec Re = 10exp 6.
Il serait hautement souhaitable qu’on n’en reste pas à ce calcul effectué il y a un demi-siècle avec l’aide de formules d’une couche limite laminaire alors que l’écoulement et sa couche limite sont turbulents.
Des mesures supplémentaires, à d’autres nombres de Reynolds seraient aussi utiles. Ce serait un simple travail d’étudiant, accédant à une soufflerie. Je l’ai suggéré aux autorités qui à l’époque avaient financé ces études, sans aucun succès: cinquante et plus ? trop vieux, obsolète.
Résultat: au bout d’un siècle de recherches intenses dans un domaine qui commande le développement de l’aviation, et de la navigation à voile, la vérité à propos d’un phénomène élémentaire, signalé depuis plus de deux siècles par Thomas Young, avec une explication élémentaire n’est toujours pas établie, avec la rigueur nécessaire pour rejeter définitivement des explications magiques avancées entre temps avec beaucoup de légèreté, parfois par des spécialistes, et pour figurer dans le Schlichting, bible de la couche limite.
J’ai représenté à nouveau en janvier 1967 mon calcul approché à la seconde conférence de Fluidique de Cambridge, qui est reproduit ci-dessous:
ABSTRACT: The curved wall effect or deflection of a jet of width h and Reynolds number Re attached to a convex wall of radius r is calculated as an effect of the separation of the boundary layer along the wall. Formulas are given both for laminar and turbulent boundary layers, in agreement with the author’s experimental results although thes are incomplete. Theory indicates an influence of the Reynolds number and predicts that the curved wall effect should disappear in the laminar case.

The curved wall effect, Cambridge Fluidics conference, 5/01/1967

The curved wall effect, Cambridge Fluidics conference, 5/01/1967

The curved wall effect, Cambridge Fluidics conference, 5/01/1967

The curved wall effect, Cambridge Fluidics conference, 5/01/1967

The curved wall effect, Cambridge Fluidics conference, 5/01/1967

The curved wall effect, Cambridge Fluidics conference, 5/01/1967

The curved wall effect, Cambridge Fluidics conference, 5/01/1967

The curved wall effect, Cambridge Fluidics conference, 5/01/1967
The curved wall effect, Cambridge Fluidics conference, 5/01/1967



